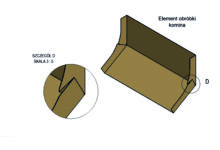
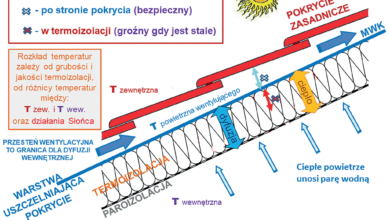
Jak to jest z tym punktem rosy?
Z pierwszej części tekstu wiemy już sporo o parze wodnej, wilgoci i wilgotności. Znamy pojęcia wilgotności bezwzględnej oraz tej istotniejszej, czyli wilgotności względnej. Omówiliśmy zjawisko nasycenia powietrza parą wodną i wyjaśniliśmy, czym jest punkt rosy, a w zasadzie temperatura punktu rosy.
Tekst i ilustracje Przemysław Spych, Anatomia dachu
Teraz zrobimy krok dalej. Omówimy wykres Molliera, który w wersji podstawowej wcale nie jest straszny, a sądzę, że co najmniej przydatny i wiele można z niego wywnioskować. Zastanowimy się także, co się dzieje w przegrodzie dachowej.
Wykres w podstawowej formie, z podstawowymi jego elementami jest pokazany na wykresie 1. Ma on oczywiście oś poziomą i pionową, ale graficznie jest ustawiony powiedzmy… niestandardowo. Takie ustawienie osi i parametrów przez Richarda Molliera daje jednak pełną czytelność i przejrzystość.
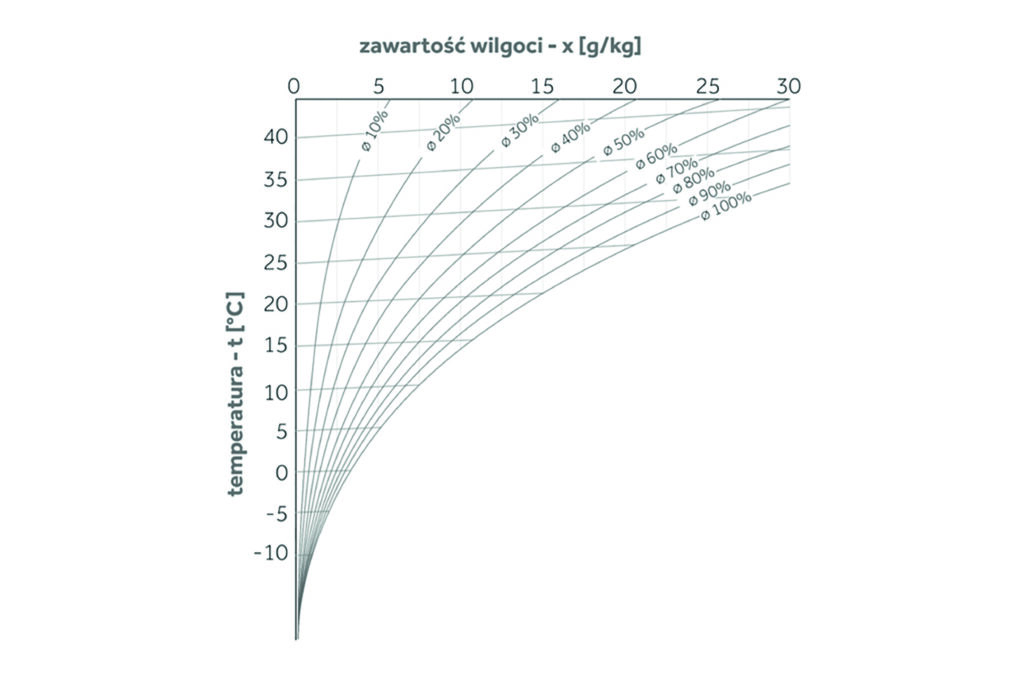
Na osi poziomej – u góry – jest parametr oznaczony jako „x”, czyli zawartość wilgoci w powietrzu. Tutaj zwracam uwagę, że w pierwszej części tekstu pisaliśmy o wagowej zawartości pary wodnej w 1 m3 powietrza. Pisaliśmy, że na przykład maksymalna zawartość pary wodnej w 1 m3 powietrza w danej temperaturze wynosi „tyle i tyle” gramów, a tutaj mamy zmianę jednostek. Otóż sprawa jest w sumie prosta. Chodzi o masę 1 m3 powietrza, czyli jego gęstość. No właśnie, wydaje się proste. Tylko, że tutaj sprawa się odrobinę komplikuje. Ale obiecuję, że tylko odrobinę i dla naszych potrzeb nie będzie to miało większego znaczenia. Tę drobną komplikację trzeba jednak wyjaśnić. Chodzi o to, że powietrze jako gaz zmienia swoje podstawowe parametry wraz z wysokością nad poziomem morza i wraz z temperaturą. Gdzie mierzyć gęstość i w jakiej temperaturze? Nad morzem latem czy na szczytach Alp zimą? Otóż jest to ustandaryzowane. Przyjmuje się, że na poziomie morza w temperaturze 20 stopni Celsjusza powietrze suche ma gęstość 1,2 kg/m3. Fizycy oczywiście nie byli usatysfakcjonowani tym wynikiem, bo zawsze jest jakieś „ale”. Wprowadzono zatem jeszcze dwie sytuacje, które można stosować jako pewną bazę, jako punkt odniesienia. Przyjęto więc pewne bazowe warunki (temperatura i ciśnienie) jako „normalne” oraz nieco inne warunki bazowe jako „standardowe”. Gęstość powietrza w „warunkach normalnych” wynosi 1,293 kg/m3. Natomiast gęstość powietrza w „warunkach standardowych” wynosi 1,225 kg/m3. Mamy zatem gęstość powietrza mieszczącą się – tutaj zaokrąglam, bo nie będziemy dokonywać odkryć na miarę Nobla – w zakresie 1,2-1,3 kg/m3. Dla perfekcjonistów to może mieć znaczenie, ale dla naszych celów zrozumienia zjawisk wilgotnościowych w powietrzu – nie. A jeśli mam być tutaj szczery, to wystarczy pamiętać, że 1 m3 powietrza waży trochę więcej niż 1 kg. Albo, że 1 kg powietrza to trochę mniej niż jego 1 m3. Dobra jestem nawet zdania, że na tę różnicę dla naszych tutaj potrzeb możemy nawet machnąć ręką. 1 = 1 też dobrze. I tyle. No chyba, że jesteś perfekcjonistą ;-).
Na osi pionowej mamy temperaturę. Tutaj kombinowania nie ma. Zwracam tylko uwagę, że linie stałej temperatury nie są równoległe do osi poziomej. Trzecim elementem wykresu są bardzo charakterystyczne krzywe biegnące ku górze i mniej lub bardziej odginające się w prawo. To linie o stałej wartości wilgotności względnej ɸ.
Jak czytać wykres Molliera?
Wykres już znasz. To teraz postawmy na nim jakąś kropkę. Wpisz w swojego wszystkowiedzącego smartfona, w wyszukiwarce, hasło pogoda na dziś albo coś podobnego. Wyskoczy Ci zapewne witryna z pewnymi danymi dotyczącymi pogody. Będzie tam na pewno temperatura i obok kilku innych parametrów także wilgotność względna. Powiedzmy, że temperatura wynosi 25 stopni Celsjusza, a wilgotność względna ɸ to 70%.
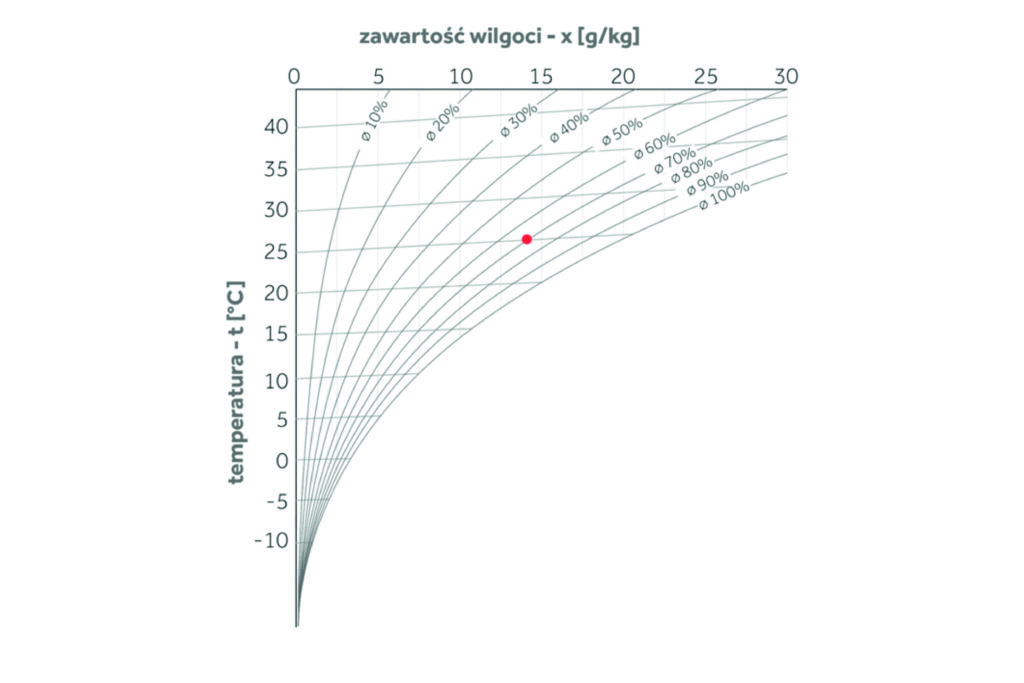
Przechodzimy do wykresu. Na skrzyżowaniu linii t = 25 stopni Celsjusza oraz ɸ = 70% stawiamy kropkę. Masz to na wykresie 2. W ten sposób określiliśmy na wykresie położenie punktu charakteryzującego stan wilgotnościowy powietrza. Mając ten punkt w łatwy sposób możemy sprawdzić, ile pary wodnej jest w powietrzu. Odczytujemy to z układu współrzędnych wykresu Molliera. W naszym konkretnym przypadku jest to mniej więcej 14 g na 1 kg powietrza. Zobacz na wykres 3.
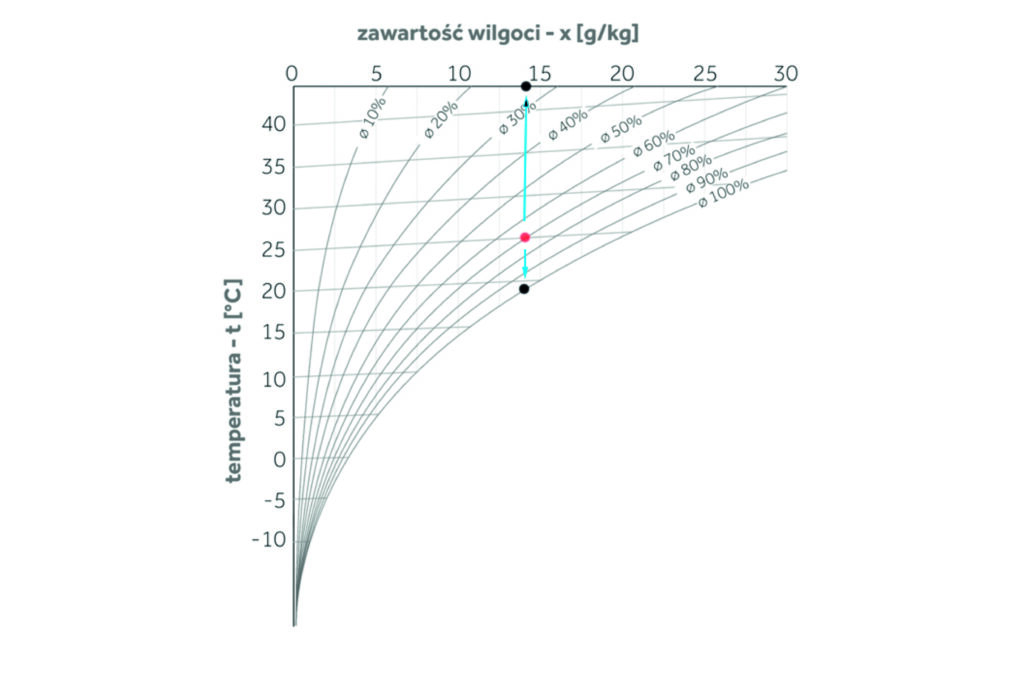
Tutaj oczywiście wiemy, że w 1 m3 będzie jej nieco więcej, bo przelicznik jest 1,2-1,3. Z wykresu możemy odczytać jeszcze jedną bardzo istotną wartość, a mianowicie to, jaka jest temperatura punktu rosy dla danej wilgotności i temperatury powietrza. Znów zerknij na wykres 3. Tę wartość odczytujemy na krzywej ɸ100%. Jest to mniej więcej 19 stopni Celsjusza. Omówmy to pokrótce. Otóż, jeśli nagle zacznie się ochładzać i temperatura z początkowych 25 stopni Celsjusza spadnie do właśnie 19 stopni Celsjusza, to powietrze osiągnie stan nasycenia parą wodną i wilgotność względna osiągnie wartość 100%. To jest temperatura punktu rosy, bo jeśli temperatura spadnie poniżej tej wartości, to powietrze już nie zmieści w sobie więcej pary wodnej i zacznie się jej pozbywać. Para wodna zacznie się wykraplać. To omówiliśmy w części pierwszej tekstu. A co by się działo, gdyby temperatura spadła jeszcze bardziej? Jakby to wyglądało na wykresie? Co udałoby się z tego wywnioskować?
Obniżmy temperaturę bardziej. Kontynuujmy już omówiony przypadek. Startujemy zatem od punktu 1, czyli temperatura 25 stopni Celsjusza i wilgotność względna ɸ70% i obniżamy temperaturę. Jest to zobrazowane na wykresie 4. Dochodzimy do punktu 2, czyli do krzywej ɸ100% wilgotności względnej i tutaj osiągamy przy 19 stopni Celsjusza temperaturę punktu rosy. Jesteśmy na granicy wykraplania. Obniżamy temperaturę dalej aż do powiedzmy 5 stopni Celsjusza, czyli do punktu 3 na wykresie. Poniżej punktu 2, wilgotność względna powietrza nie może przekroczyć 100%, więc w dół poruszamy się po krzywej ɸ100% aż osiągniemy założoną i docelową temperaturę 5 stopni Celsjusza. Jesteśmy w punkcie 3 na wykresie. Zastanówmy się teraz czego nam brakuje do pełnego obrazu w punkcie 3?
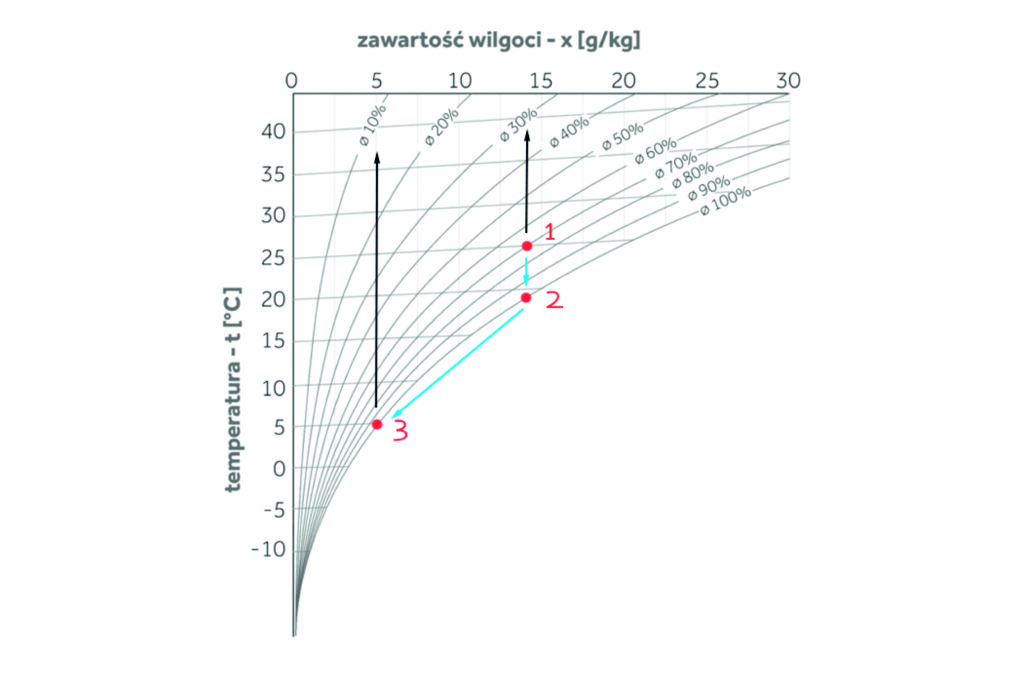
Mamy temperaturę 5 stopni Celsjusza, mamy wilgotność względną ɸ100%, brakuje zawartości wilgoci w powietrzu. Odczytamy to na osi „x” w gramach pary wodnej na 1 kg powietrza. W punkcie 3 zawartość pary wodnej w powietrzu wynosi 5 g/kg. Tak, pamiętamy o ewentualnym przeliczniku 1,2-1,3 w stosunku do 1 m3 powietrza. W punkcie 1 i w punkcie 2 zawartość pary wodnej wynosiła 14 g/kg, w punkcie 3 wynosi 5 g/kg. Co się stało z resztą? Reszta się wykropliła. Poniżej krzywej ɸ100% jest strefa mgły, strefa wykraplania. Możemy nawet w banalny sposób policzyć, ile tej pary wodnej się wykropliło, odejmujemy 5 od 14 i mamy 9 g pary wodnej, która wykropliła się z każdego 1 kg powietrza. Tak, z każdego 1 m3 wykropliło się o 20-30% więcej, bo jest ten przelicznik 1,2-1,3. Czy to jest dużo czy mało, trudno powiedzieć.
Spróbujmy to jeszcze oszacować „globalnie” dla dachu. Policzmy to. Tym razem zachowamy pewną dokładność. Przyjmijmy, że obliczenia przeprowadzimy dla przegrody dachowej o powierzchni 100 m2 i izolacji o grubości 30 cm ograniczonej z jednej strony membraną otwartą dyfuzyjnie, a z drugiej paroizolacją. Przyjmijmy, że izolacja to materiał, w którym izolatorem jest powietrze. Przyjmijmy, że w tej izolacji 1/3 jej objętości to „materiał własny” izolacji, a 2/3 to powietrze w tej izolacji. Dla ułatwienia pomińmy krokwie. Zatem, jeśli mamy warstwę 30 cm, to przyjmijmy za powyższymi założeniami, że powietrza jest w niej 20 cm. To teraz możemy policzyć, jaka jest objętość powietrza w 100 m2 tej przegrody:
100 m2 x 0,2 m = 20 m3
Teraz zważmy to powietrze, ale już z pewną dokładnością. Wiemy, że 1 m3 powietrza suchego waży około 1,2-1,3 kg, przyjmijmy, że 1,25. Zatem 20 m3 będzie ważyło:
20 x 1,25 = 25 kg
Z każdego kilograma powietrza w naszym przykładzie z wykresu 4 wykropliło się 9 g. Zatem z 25 kg powietrza wykropliłoby się 25 x 9, czyli około 225 g. Kubek wody. Na 100 m2. Chyba niedużo. To był taki przykład, gdzie całe powietrze zawarte w przegrodzie (izolacji) ma wilgotność względną 70% i temperaturę 25 stopni Celsjusza i nagle ochładza się do 5 stopni Celsjusza, co jest mało prawdopodobne. Wykroploną wodę trzeba by wlać do spryskiwacza i rozpylić na powierzchni tych 100 m2, a w zasadzie to nie na jej powierzchni tylko dodatkowo na jej „grubości”. Wyschłoby szybko. Czy taki efekt wykraplania pary wodnej w izolacji jest groźny?
Efekty punktu rosy w warstwach dachu
Najważniejsze jest to, że takie zjawisko w przegrodzie dachowej występuje okresowo. Najbardziej sprzyjające warunki są jesienią. Zawilgocenie izolacji, jej górnej warstwy, jest możliwe i wręcz dopuszczalne. Niebezpieczne jest długotrwałe nawarstwianie się, powtarzanie, kumulowanie zjawiska. Groźne są mostki termiczne i zaniedbania w ich okolicy. W mostkach termicznych zjawisko wykraplania występuje nawet obficie. Woda jest dobrym przewodnikiem ciepła, więc dodatkowo potrafi wzmocnić efekt. Woda powoduje butwienie i erozję drewna. W zawilgoconych i ciepłych warunkach rozwijają się też grzyby. Zaniedbania mogą więc prowadzić do przykrych i kosztownych rezultatów. Jeśli natomiast przegroda dachowa jest zaizolowana poprawnie, wyposażona w membranę otwartą dyfuzyjnie i paroizolację (taką czy inną) oraz sprawną wentylację nad tą membraną i wewnątrz budynku, to wszystko działa dobrze i w skali roku zawilgocona izolacja szybko wysycha.
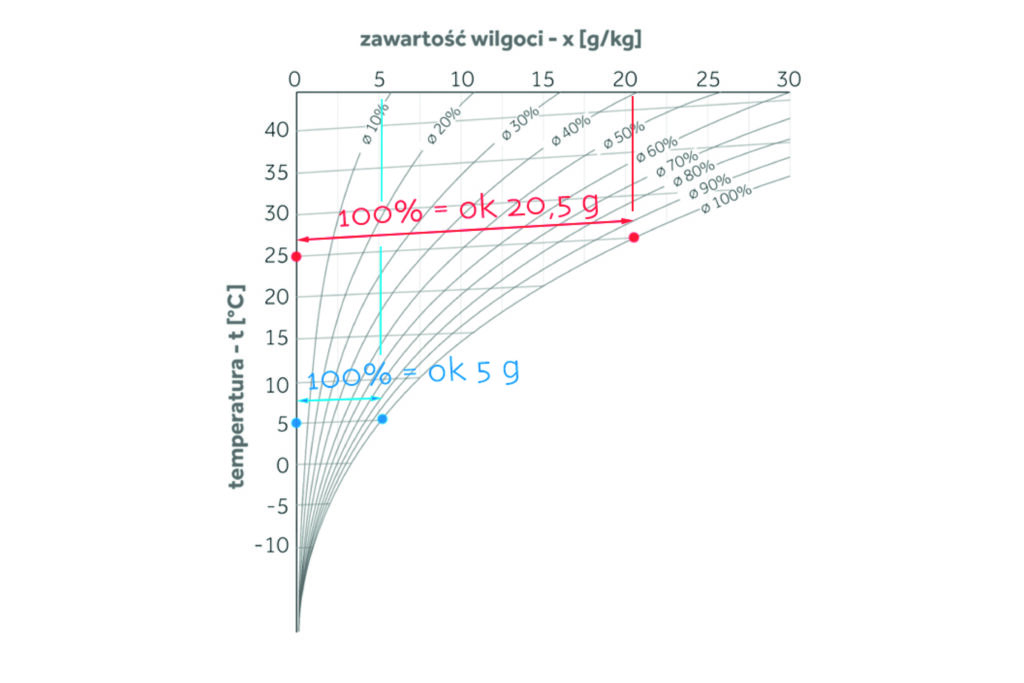
Na koniec popatrzmy jeszcze na wykres 5. Zwróćmy uwagę na bardzo istotną kwestię, o której już w pierwszej części mówiliśmy. Otóż pojemność powietrza spada wraz z temperaturą. No tak, ale dopiero na wykresie Molliera widać wyraźnie, że spada ogromnie. Czym innym jest 70% wilgotności względnej przy temperaturze 25 stopni Celsjusza czy 30 stopni Celsjusza, a czym innym 70% przy temperaturze +5 stopni Celsjusza czy –5 stopni Celsjusza. Pojemność spada wielokrotnie. Im niższa temperatura, tym mocno „ciaśniejszy” jest ten zakres.
Podsumowanie
Teraz już wiesz, jak z tego uproszczonego wykresu Molliera korzystać. W sumie to proste. W Internecie można znaleźć wykresy Molliera z dużo większą zawartością danych czy liczbą linii. Ale zawsze znajdziesz na nich to, co omówiliśmy przed chwilą. I wiesz już więcej.